309 words
2 minutes
[CS5446] Game Theory
Elements of a game
- Players (N): set of decision makers
- Actions (): possible actions for each player
- : combination of actions
- Payoffs (): reward for layer based on action
- Information (): what player knows about the game
- Strategy (): plan of action for player based on its known information
- Objective: to choose optimal strategy that maximizes payodd, given strategy of others .
- Equilibrum (): stable outcome where no player can improve payoff by changing strategy
Type of game
- Non-cooperative vs. Cooperative
- Simultaneous vs. Sequential
- Perfect vs. Imperfect information
- Single vs. Repeated game
Non-Cooperative game
Game of pure competition
- players have opposing interests
- involve 2 players
- the sum of payoffs is a constant:
- payoff sum of zero-sum game is
Game of pure coordination
- players have same interests
- all players aim for the same outcomes
- all players have the same playoffs:
Pure strategy game
Players choose simultaneously, with immediate outcome
example: Prisoner’s dilemma
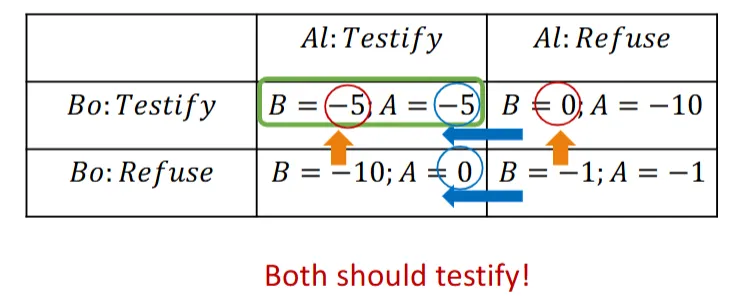
Solution: a strategy profile where each player adopts a rational strategy.
- Pareto Optimal: No player can be made better off without making anotherplayer worse off
- Nash Equilibrium: No player can improve their payoff by unilaterally changing their strategy: for all and
- every game has at least one Nash equilibrium

- every game has at least one Nash equilibrium
Domination
- Dominant Strategy: strategy dominates all others if it always yoelds a better or equal outcome regardless of other playes’ strategies
- Strongly dominant strategy:
- Weakly dominant strategy:
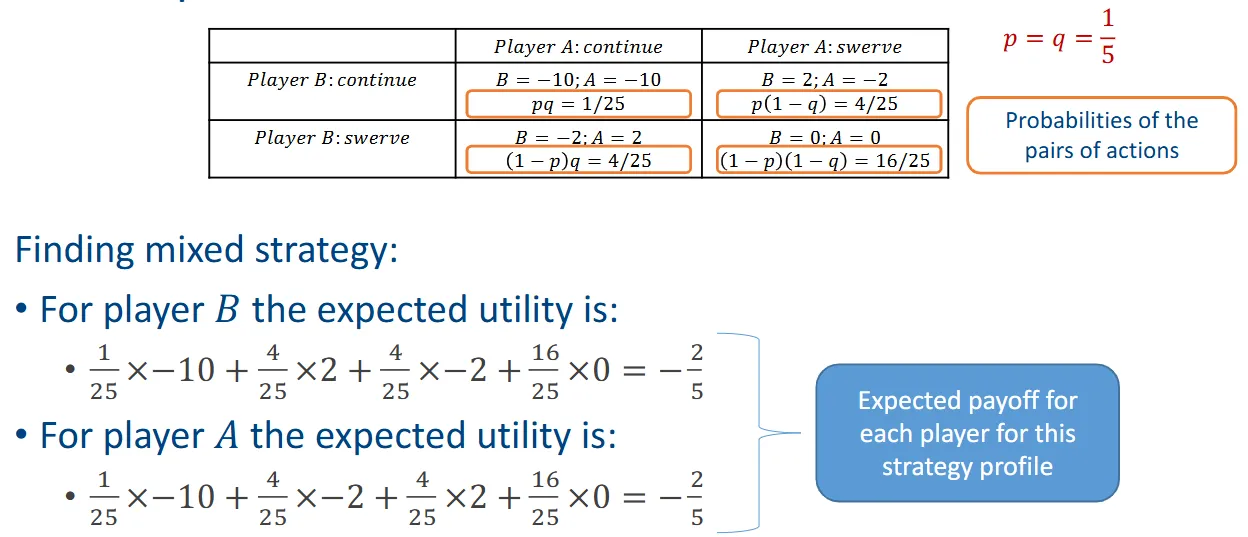
Mixed strategy game
Probabilistic action selection with randomized policy
- Example: game of chicken
Zero-sum game
- Minimax Theorem
- in a finite, two-player zero-sum game, the maximin value (the maximum of a player’s minimum payoffs) is equal to the minimax value (the minimum of the opponent’s maximum payoffs) 0 both players have optimal mixed strategies that ensure the same game value, regardless of the order of play
[CS5446] Game Theory
https://itsjeremyhsieh.github.io/posts/cs5446-9-game-theory/