315 words
2 minutes
[CS5446] Partial Observable Markov Decision Process
POMDP
- uncertainty in observations
- agent doesn’t konw exactly which state it is in
- : state
- : action
- : evidence/ observation
- : transition function
- : observation function
- (probability of observing from state , defines the sensor model)
- : reward function
- history
- policy:
- define on belief state or
- define on history
Belief state
- actual state is unknown, but we can track the proability distribution over possible states
- : probability of agent is now in actual state by belief
- belief update: (filtering)
- agent executes , receives evidence , then update
Decision making of POMDP
- give current belief , execute action
- receive evidence
- update belief
Belief space MDP
reducing POMDP into MDP
- transition model
- reward function
- each belief is a state
Solution for POMDP
- Discretize the belief state space
- construct belief space MDP
- discretize belief state space
- solve the MDP
- map the solution back to POMDP
- ( is discretized)
- problem: Curse of dimensionality (state sapce too large, even after discretization)
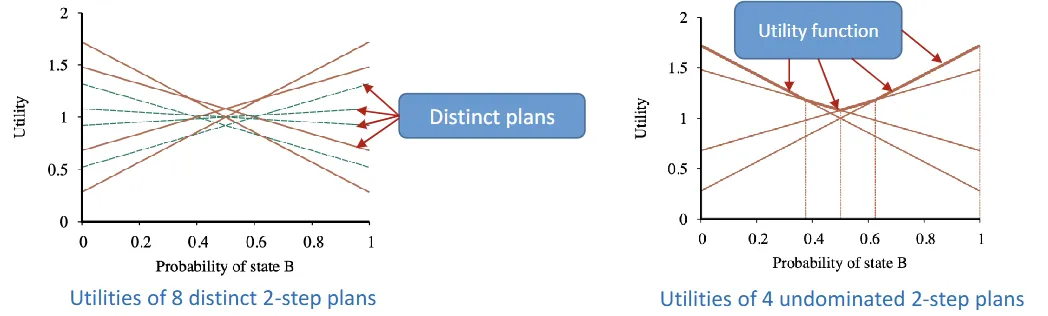
- Utility function representaed by piecewise linear function
- conditional plan: policy generates action observation update belief state new action … The conditional plan is the policy
- utility function of belief state
- : utilify of executing a conditional plan starting in real state
- expected utility of executing in belief state :
- maximum of collection of hyperplanes piecewise linear, or convex
- continuous belief space is divided into regions
Online methods (Approximation solutions)
- to scale up
- POMCP (Partially Observable Monte Carlo Planning)
- run UCT on POMDP, uses action-observation history
- samples a state at root from the initial belief
- select expand simulate backup
- DESPOT (Determinized Sparse Partially Observable Tree)
- similar to POMCP, but at every observation node, only sample a single observation (make the tree smaller)
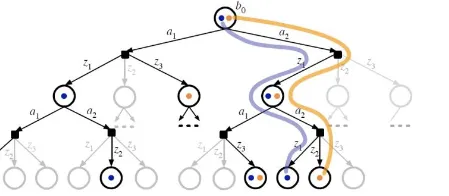
- similar to POMCP, but at every observation node, only sample a single observation (make the tree smaller)
[CS5446] Partial Observable Markov Decision Process
https://itsjeremyhsieh.github.io/posts/cs5446-8-partial-observable-mdp/