Model-free vs. Model-based#

• Model-free: No model, learn value function from experience
• Model-based:
  • Model the environment
  • Learn/ Plan value function from model and/ or experience
  • Efficient use of data
  • Reason about model uncertainty
  • But may have model bias

Model#

• $(S, A, T, R, \gamma)$ parameterizad by $\eta$: $M_{\eta}$
• state & action are known
• find transition & reward function (unknown)
• model learning to create model

Model Learning#

• learn from past experience $S-A-R$
• supervised learning
• to minimize loss function (MSE, KL-diverge)

Model#

1. Table Lookup Model
   • i.e ADP
   • cannot scale
2. Linear Model
   • represent tranition & reward function as linear model
3. Nearual Networks Model
   • i.e VAE

• Problem
  • learning transition function may be difficult
    • too many factors to learn from the environment
  • Sol: Value Equivalence Principle
    • Two models are value equivalent if they yielf the same Bellman updates
    • learn latent mapping function $h: s \rightarrow z$
      learn latent transition & reward function $g: z, a \rightarrow z', r$

Now that we have a model, how can we use it?

Model based techniques#

• Goal: find optimal policy/ value using the model and/or the environment

1. Direct model solving
   • solve using MDP solvers
     • i.e. value/ policy iteration
   • uses the model fully (use as if it were the environment)
   • ADP: learn a model and solve the bellman equation of the learned model
   • Value iteration network: value iteration + NN
2. Sample-based planning
   • use the model ONLY to generate samples
   • don’t consider the probability distribution of the model
     • $s' \sim P_\eta (s' | s,a)$
       $r = R_\eta (s,a,s')$
   • apply model-free RL on samples
     • Monte Carlo control
     • Q-Learning
       • but too time consuming
       • Sol: plan for states that are relevant for NOW (planning for surrounding)
3. Model-based Data Generation
   • consider both
     • real experience from environment
     • simulated experience from model
   • train model free RL with both experience
   • i.e
     • Dyna-Q
       
     • Dyna-Q+
       • Dyna-Q with exploration bonus

Frontiers#

• General Value Function (GVF)
  • generalize value function to predict any signals
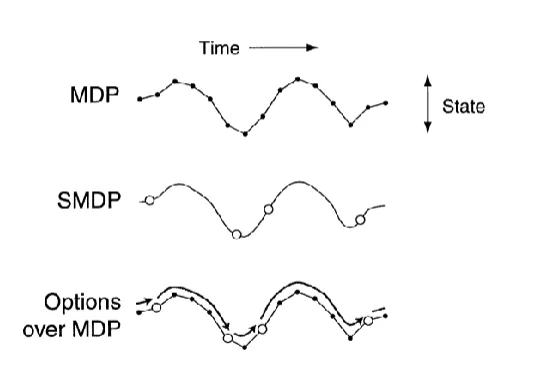
• Temporal Abstractions via Options
  • hierarchical RL
  • option $O = (I, \pi, \beta)$
    • $I \subseteq s$ (state)
    • $\pi: S \times A \rightarrow [0, 1]$: a policy to follow
    • $\beta: S \rightarrow [0, 1]$: probability of terminating at each state
• Designing Reward Signals
  • Problem: agent cannot learn until it reaches the goal (where the reward is)
  • Sol: add fake rewards to make the learning easier
  • Extrinsic reward: rewards from the environment
    Intrinsic reward: rewards from the agent itself based on its internal state