Reinforcement Learning#

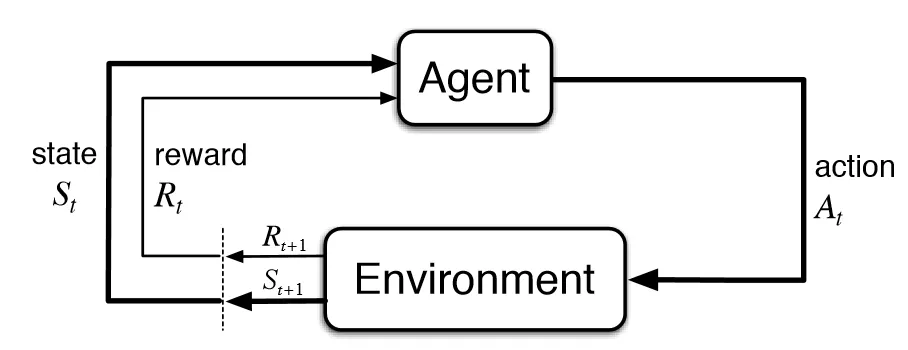
• Learning to behave in unfamiliar environment
• Environment is a Markov Decision Process
  • relies on Markov Property (but doesn’t know what it looks like)
• Unknown transition function, unknown reward function
• Use observed rewards to learn optimal policy

Types of RL#

Model-based vs. Model-free#

• Model-based: Learn transition model to solve problem
• Model-free: Doesn’t learn the transition model, directly solve the problem

Passive vs. Active learning agent#

• Passive: given policy → evaluate the value & find utility function
• Active: Learns the optimal policy & utility function.
  • Needs to balance between exploitation & exploration

Passive RL#

• Execute a set of trials using fixed (given) policy $\pi$
• Learn expected utility $U^{\pi}(s)$ for each non-terminal state $s$
  • $U^{\pi}(s) = E[\sum_{t} γ^t R(s_t, \pi(s), s_{t+1}]$

Model-based Passive RL#

1. Adaptive Dynamic Programming (ADP)

• Learn transition function through experience
  • Count outcomes of each state, action
  • Normalize to estimate $P(s'|s,a)$
• e.g
  • $𝑃(𝑠′=(3,2)|𝑠 = (3,3), 𝑎 = 𝑅𝑖𝑔ℎ𝑡) = \frac {1}{3}$
  • $𝑃(𝑠′=(4,3)|𝑠 = (3,3), 𝑎 = 𝑅𝑖𝑔ℎ𝑡) = \frac {2}{3}$
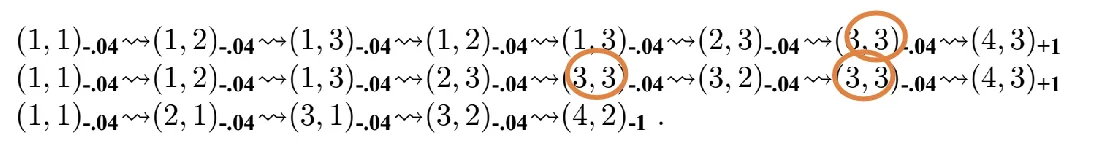
• Now we have the transition functions, we can obtain rewards for each $(s, a)$ with given policy $\pi$
  • $U^{\pi}(s) = \sum_{s'} P(s'|s, \pi(s))[R(s, \pi(s),s') + γU^{\pi}(s')]$
  • Learn reward function $R(s,a,s')$ upon entering state $s'$
  • Solve $S$ linear equations with $S$ unknowns requires $O(S^3)$ time
• Adjusts the state to agree with ALL successors
• 

Model-free Passive RL#

Directly learn the utility, doesn’t learn the transition and reward function

1. Monte Carlo Learning
   • Maintain running average of expected return for each state.
   • If run many times → converge to true expected value
   • e.g
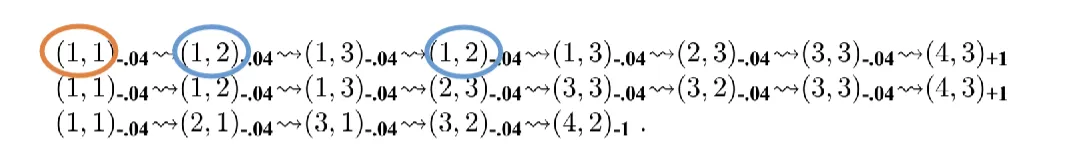
     • For the first trial,
       • Expected reward of (1,1) = 0.72
       • Expected reward of (1,2) = 0.76, 0.84
     • Overall (average),
       • $U^{\pi}(1,1) = \frac {0.72+0.72-1.24}{3} = -0.067$
       • $U^{\pi}(1,2) = \frac {0.76+0.84+0.76}{3} = 0.79$
   • Different variences: first visit vs. every visit (of a trial)
   • Slow convergence
     • Learning starts only at the end of each trial (episode)
2. Temporal Difference (TD) Learning
   • TD target: $R(s, \pi(s),s') + γU^{\pi}(s')$
   • TD error (term): TD target $- U^{\pi}(s)$
   • $U^{\pi}(s) ← U^{\pi}(s) + α($ TD Error $)$
   • N-step TD: do estimate up to $n$ steps
   • TD(λ): combine returns from different TD-steps

Active RL#

Act optimally based on prediction of utility of states

• Goal: learn optimal $\pi^*$ that obeys Bellman Equation

Model-based Active RL#

Learn the transition and reward function, then solve the MDP ($\pi^*$)

1. Active Adaptive Dynamic Programming
   • Learn model with outcome probability for all actions
   • $\pi^*(s) = argmax_{a} \sum_{s'} P(s'|s,a) [R(s,a,s')+ γ U(s')]$
   • Resulting algorithm is greedy
     • Pure exploitation may not be optimal
   • We need tradeoff between exploration & exploitation

Greedy in the Limit of Infinite Exploration (GLIE)#

• a learning policy
• scheme for balancing exploration & exploitation
• ε-greedy exploration
  • choose greedy action with $p=(1-ε)$
  • choose exploit (random) action with $p=ε$
  • lower ε over time $ε = \frac {1}{t}$, eventually becomes greedy (takes the optimal action)

Model-free Active RL#

Directly learn $\pi^*$

1. Monte Carlo Control

   • $Q(s, a) = avg( Returns(s,a))$
   • $\pi(s) = argmax_{a}f(Q(s,a), N(s,a))$
     • Exploration function $f(u,n)$
       • how greed is trade off against curiosity
       • should increase with $u$ and decrease with $n$
       • e.g
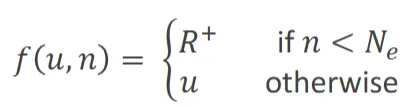
         • $R^+$: best possible reward
         • $Ne$: agent tries each state-action pair $Ne$ times

2. Active TD / TD Control

   • $Q(s,a) ← Q(s,a) + α(R(s,a,s') + γQ(s', \pi(s'))-Q(s,a))$

   Q-Learning#

   • Use optimal $\pi$ to estimate Q
   • $Q(s,a) ← Q(s,a) + α(R(s,a,s') + γmax_{a'} Q(s,a')-Q(s,a))$
   • off-policy: estimate policy ≠ behavior policy
   • Q-function: expected total discounted reward if $a$ is taken in $s$ with optimal behavior
     • $U(s) = max_a Q(s,a)$

   SARSA (State-Action-Reward-State-Action)#

   • Uses TD for prediction, ε-greedy for action selection
   • $Q(s,a) ← Q(s,a) + α(R(s,a,s') + γQ(s',a')-Q(s,a))$
   • on-policy
   • Waits until an action is taken, then update Q function

Comparison#