Decision Making under Uncertainty#

• Decision Algorithm
  • Input: a problem
  • Output: a solution (policy) that specifies best action in each state wrt. values
• Types of decision theory
  1. Normative decision theory: describes how ideal, rational agents should behave
  2. Descriptive decision theory: describes how actual agents aka humans really behave
  3. Prescriptive decision theory: guidelines for agents to behave rationally
• environment: episodic, non-deterministic, partially observable
• try to maximize gain
• Decision Model:
  • Actions: $a \in A$
  • States: $s \in S$ with probability of reaching: $P(s)$
  • Transition model: $P(s'|s, a)$ probability that action $a$ in state $s$ reaches state $s'$
  • Result: $Result(a)$
  • Probability of outcome state $s'$: $P(Result(a) = s') = \sum_{s} P(s)P(s'|s,a)$
  • Utility function: $U(s)$ express the desirability of a state $s$
• rational: to maximize the maximum expected utility (MEU)
• EU of action: average of utility value for all outcomes, weighted by probability
  • $EU(a) = \sum_{s'}P(Result(a) = s')U(s') = \sum_{s'} \sum_{s} P(s)P(s'|s, a)U(s')$

Axioms of Utility#

• notation:
  • $A ≻ B$: agent prefers A to B
  • $A ∼ B$: agent is indifferent between A and B
  • $A ≽ B$: agent prefers A over B or is indifferent between them
• 6 rules
  • Orderability: must be one of $A ≻ B$, $A∼B$, or $B ≻ A$
  • Transitivity: If $A ≻ B ∧ B ≻ C$ => $A ∧ C$
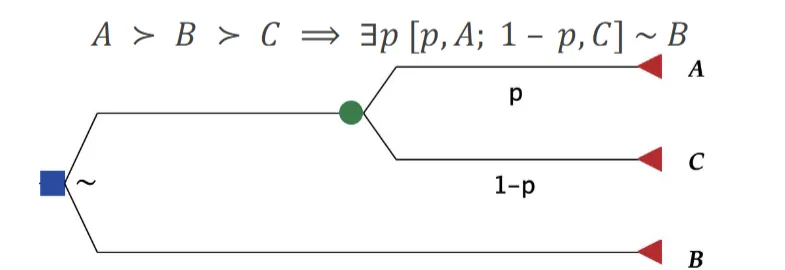
  • Continuity: If $A ≻ B ≻ C$ => there exist some probability $p$ for which the agent will be indifferent between
    1. getting $B$ for sure
    2. getting the lottery that gets $A$ with probability $p$ and $C$ with probability $1-p$
    • 
  • Substitutability: If $A ∼ B$ => $[p, A; 1-p, C] ∼ [p, B; 1-p, C]$
  • Monotonicity: If $A ≻ B$ and $p > q$ => $[p, A; 1-p, B] ≻ [q, A; 1-q, B]$
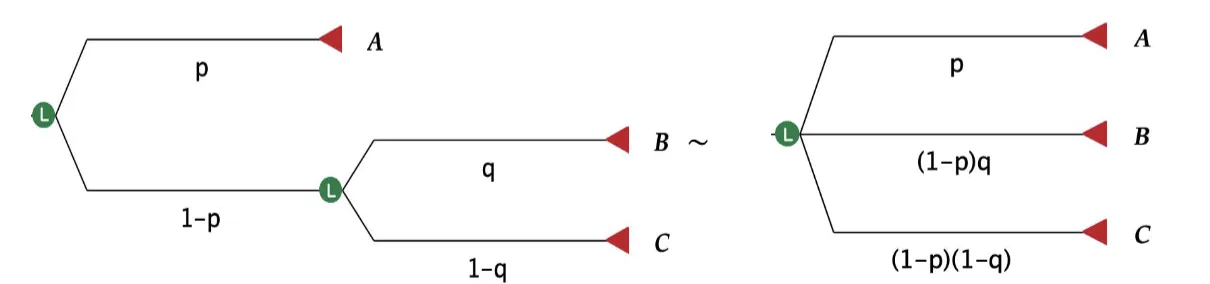
  • Decomposibility:
    • 
• $𝑈(𝐴) > 𝑈(𝐵) ⟺ 𝐴 ≻ 𝐵$, $𝑈(𝐴) = 𝑈(𝐵) ⟺ 𝐴 ∼ 𝐵$

NOTE

Agent’s behavior doesn’t change if $U$ is subjected to an affine transformation
$U'(s) = aU(s) + b$ with $a > 0$

Utility function#

• encode preferences
• translate “desirability” measures $x$ into utility units $U(x)$

Preference elicitation methods#

How to get the utility?

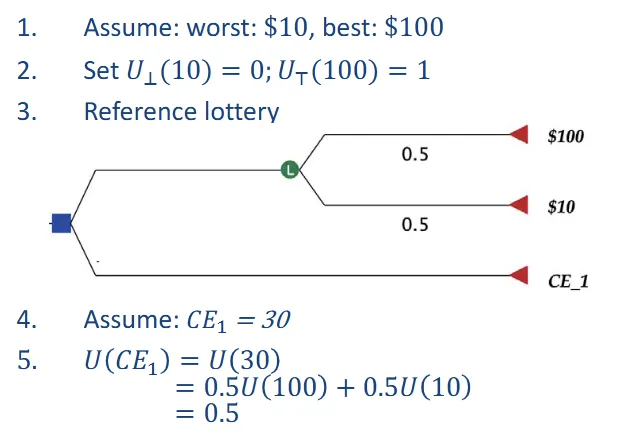
1. Probability equivalent
   • set $u_{\perp} = 0; u_{\tau} = 1$
   • find $p$ s.t $U(s) ∼ [p, u_{\tau} ; 1-p, u_{\perp}] \Rightarrow U(s) = p$
   • 最好的設成1，最差的設成0，如果選擇$s$的機率等於選擇$[p$機率是最好的，$(1-p)$機率是最差的$]$，那麼選擇$s$的utility是$p$, $U(s) = p$
2. Certainty Equivalent (CE)
   • how much $ the lottery is equivalent to in your mind.
   • $U(CE) = EU(Lottery)$
   • 

Expected Monetary Value (EMV)#

• use money as decision objective
• doesn’t take into account risk attitude
• e.g. Win 1 million so far. A lottery: 50% loss all, 50% add 1.5 million. Play?
  $\Rightarrow [0.5, 0; 0.5, 2.5] = 1.25 > 1$, Play!

Risk Attitude and Risk Premium#

• Risk_premium = EMV - CE
  • how much money are you willing to buy the lottery?
• Risk-averse: $EMV > CE$, $RiskPremium > 0$ (不想吃虧)
• Risk-seeking: $EMV < CE$, $RiskPremium < 0$ (賭下去就對了)
• Risk neutral: $EMV = CE$, $RiskPremium = 0$