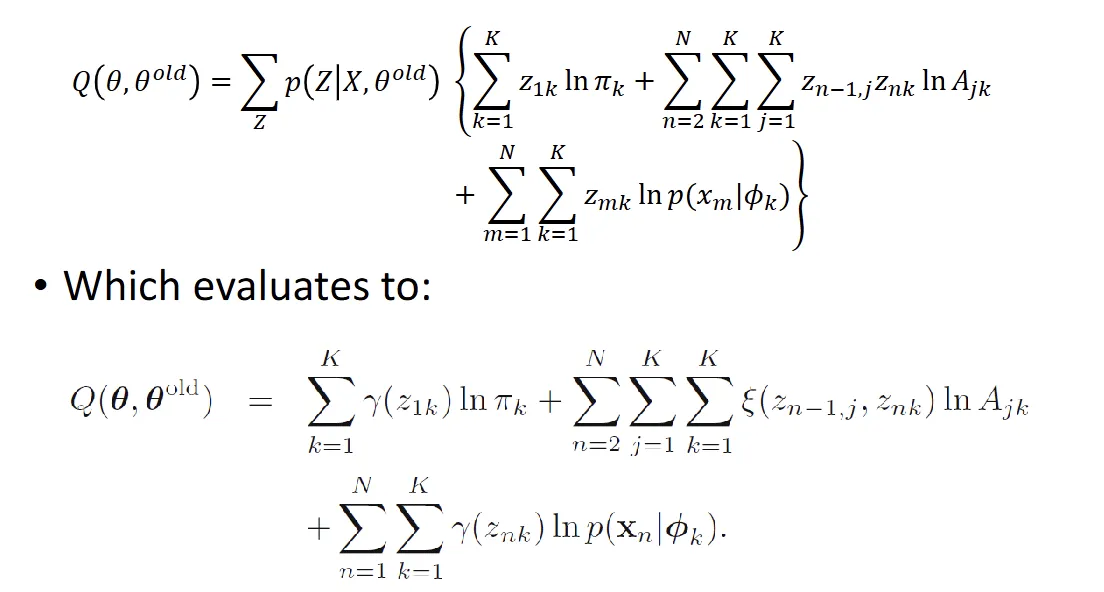HMM#

an extension of mixture model
choice of mixture component depends on the previous observation
latent variables $\{ Z_1, ..., Z_{n-1}, Z_n, ... \}$ ${Z_{1}, ..., Z_{n - 1}, Z_{n}, ...}$ form a Markov Chain, where the current state $Z_n$ $Z_{n}$ is dependent on the previous state $Z_{n-1}$ $Z_{n - 1}$
- $Z_{n+1} \perp Z_{n-1} | Z_n$
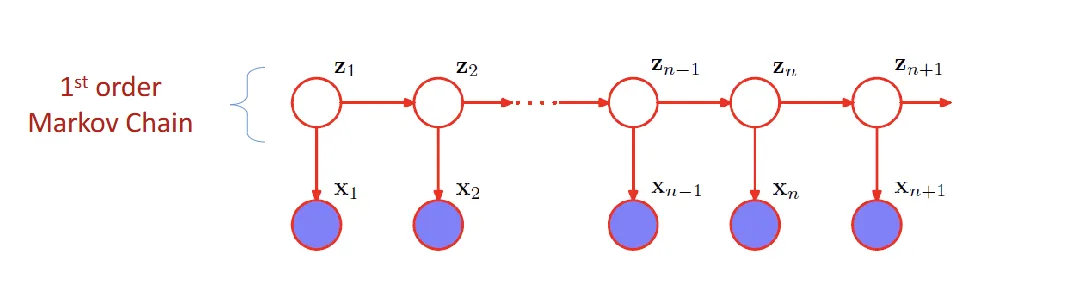
- $p(x_1, ..., x_N, Z_1, ... Z_N) = p(Z_1) \prod_{n=2}^N p(Z_n|Z_{n-1}) \prod_{n=1}^N p(X_n|Z_n)$

Transition probabilities#

1-of-K coding
describe which component of the mixture model is responsible for generating the corresponding $x_n$
$Z_n \in {0, 1}^K$ , $p(Z_n | Z_{n-1})$ is a $K \times K$ matrix. ( $A$ )
$A_{jk} = p(Z_{n,k} = 1| Z_{n-1, j}=1)$ $A_{jk} = p (Z_{n, k} = 1∣ Z_{n - 1, j} = 1)$
- $A_{jk}$ : state $j$ to state $k$
- $Z_{n,k}=1$ : $Z_n$ is state $k$
- $Z_{n-1, j}=1$ : $Z_{n-1}$ is state $j$
- $0 \leq A_{jk} \leq 1, \ \sum_K A_{jk}=1$
$p(Z_n|Z_{n-1},A) = \prod_{k=1}^K \prod_{j=1}^K A_{jk}^{Z_{n-1,j} \times Z_{n,k}}$ $p (Z_{n} ∣ Z_{n - 1}, A) = \prod_{k = 1}^{K} \prod_{j = 1}^{K} A_{jk}^{Z_{n - 1, j} \times Z_{n, k}}$
- $Z_n$ is state $k$ and $Z_{n-1}$ is state $j$
$p(Z_1 | \pi) = \prod_{k=1}^K \pi_k^{Z_1,k}$ $p (Z_{1} ∣ π) = \prod_{k = 1}^{K} π_{k}^{Z_{1}, k}$ where $\sum_K \pi_k = 1$ $\sum_{K} π_{k} = 1$
- $\pi_k$ : probability of categorical distribution

$p(X_n | Z_n, \phi)$ $p (X_{n} ∣ Z_{n}, ϕ)$
- $\phi$ : parameters governing the distribution
- $p(x_n | Z_n, \phi) = \prod_{k=1}^K p(x_n| \phi)^Z_{nk}$ $p (x_{n} ∣ Z_{n}, ϕ) = \prod_{k = 1}^{K} p (x_{n} ∣ ϕ)_{nk}^{Z}$
  - $Z_n$ is $k$ state, only one $Z_{nk}$ will be 1

all conditional distributions governing latent variables share the same parameters $A$
all emission distributions share the same parameters $\phi$

now we want to find the maximum likelihood $p(x| \theta) = \sum_Z p(x,z| \theta)$
NO closed-form solutions
$\Rightarrow$ use EM algorithm

Initialization of parameters $\theta^{old}$
E-step: find $Q(\theta, \theta^{old}) = \sum_Z p(z| x, \theta^{old}) ln \ p(x, z| \theta)$ $Q (θ, θ^{o l d}) = \sum_{Z} p (z ∣ x, θ^{o l d}) l n p (x, z ∣ θ)$
- we define:
  - $r(z_n) = p(z_n | x, \theta^{old})$
  - $r(z_{nk})$ $r (z_{nk})$ : conditional probability of $z_{nk} = 1$ $z_{nk} = 1$
    - $= E[z_{nk}] = \sum_{z_n} r(z_n)z_{nk}$
    - $z_{nk}=1$ when $k=k$
  - $\xi(z_{n-1}, z_n) = p(z_{n-1}, z_n | x, \theta^{old})$
  - $\xi(z_{n-1,j}, z_{n,k}) = E[z_{n-1,j}, z_{n,k}]= \sum_{z_{n-1}, z_n} \xi(z_{n-1}, z_n) z_{n-1,j} z_{n,k}$
- our goal is to compute
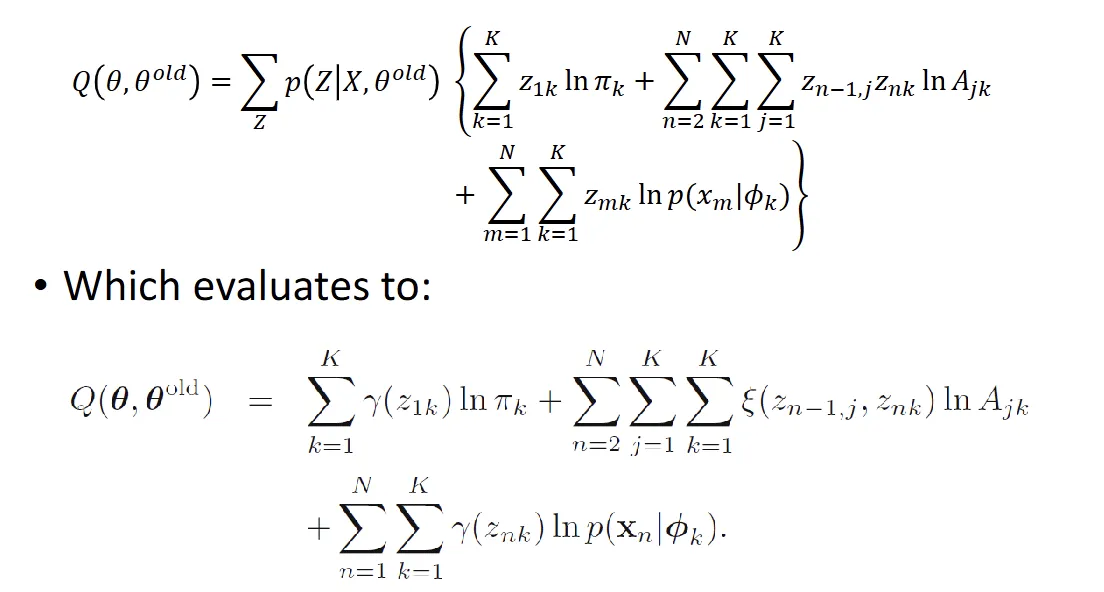
  - therefore to find $r(z_n)$ and $\xi(z_{n-1,j},z_{n,k})$
- using the Forward-Backward algorithm to find $\alpha$ and $\beta$
- $\alpha(z_n) = p(x_n|z_n) \sum_{z_{n-1}} \alpha(z_{n-1}) p(z_n|z_{n-1}$
- $\beta(z_n) = \sum_{z_{n-1}} \beta(z_n+1) p(x_{n+1}|z_{n+1} p(z_{n+1} |z_n)$
- $\alpha(z_{1,k})$ for $k=1, ... ,K$ $=\pi_k p(x_1 | \phi_k)$
- $\beta(z_n) =1$
M-step: maximize $Q(\theta, \theta^{old})$ $Q (θ, θ^{o l d})$ w.r.t $\theta = \{ \pi, A, \phi \}$ $θ = {π, A, ϕ}$
- $\pi_k = \frac {r(z_{1k})}{\sum_{j=1}^K r(z_{1j})}$
- $A_{jk} = \frac {\sum_{n=2}^N \xi(z_{n-1,j}, z_{n,k})}{\sum_{l=1}^K} \sum_{n=2}^N \xi(z_{n-1,j} z_{n,l})$

values of $\alpha(z_n)$ can go to $0$ exponentially quickly
$\hat \alpha(z_n) = p(z_n| x_1, ..., x_N) = \frac {\alpha(z_n)}{p(x_1,..., x_N)} = \frac {\alpha(z_n)}{C_n}$ $\overset{α}{^} (z_{n}) = p (z_{n} ∣ x_{1}, ..., x_{N}) = \frac{α ( z _{n} )}{p ( x _{1} , ... , x _{N} )} = \frac{α ( z _{n} )}{C _{n}}$
- $C_n = p(x_1,..., x_N)$
$\hat \beta(z_n) = \frac {\beta(z_n)}{C_{n+1}}$
$\Rightarrow$ $\Rightarrow$
- $r(z_n) = \hat \alpha(z_n) \hat \beta(z_n)$
- $\xi(z_{n-1}, z_n) = C_n^{-1} \hat \alpha(z_{n-1}) p(x_n | z_n) p(z_n | z_{n-1}) \hat \beta(z_n)$