492 words
2 minutes
[CS5340] Factor Graph & Junction Tree Algorithm
Factor Graph
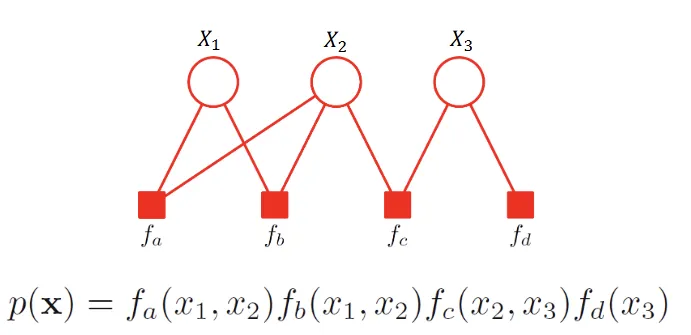
- to explicitedly show details of factorization
- Variable + Factor nodes
- : random variable (circle)
- : factors (square)
- : undirected edges, factor to all variable it depends on
DGM to factor graph:
- parent-child relationship
UGM to factor graph:
- maximum clique
- can remove since can define it over empty set of variables
NOTEfactor graph representation is not unique
- DGM / UGM with local cycles can become tree
- therefore can run sum-product algorithm
- therefore can run sum-product algorithm
Sum-Product algorithm on factor graph
- Goal: compute all singleton marginal probability
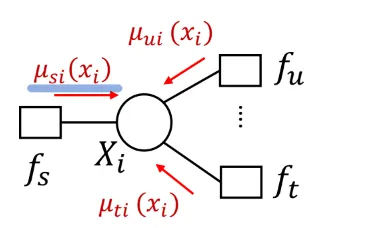
- Message:
- : variable to factor node
- no marginalization
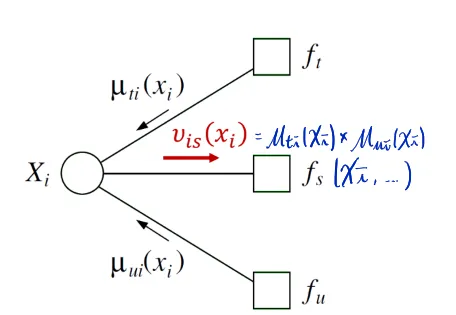
- : factor to variable node
- should contain only , marginaliza away all other nodes
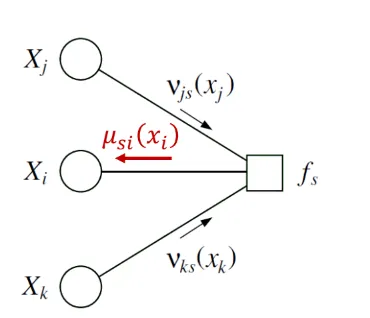
- message from leaf node (Initialization)
- : variable to factor node
- Marginal probability
-
Maximum a Posterior (MAP) problem
- Goal: to maximize over all sets of random variables
- find the maximal probability
- find the configuration
- ( can be removed)
CAUTIONUnderflow problem: prodects of
- Solution: log scale,
(becomes Max-Sum algorithm)
Max-Product Algorithm
Or Max-Sum algorithm if using log scale
- similar to Sum-Product algorithm
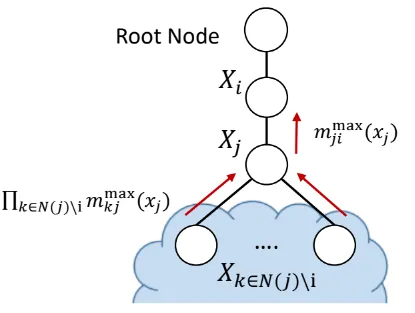
- inward message
-
Getting the configurations
- also record max configuration per inward message
- track the configurations from root as outward process
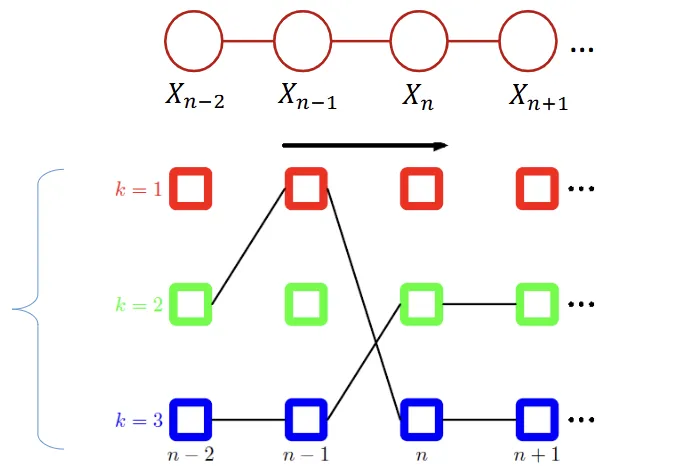
- Trellis diagram
Junction Tree (Clique Tree)
- Probability distributions of a loopy undirected graph can be re-parameterizes as trees can perform Sum-Product algorithm
- Cluster graph Cluster tree Junction tree
- Cluster graph
- cluster nodes edges between sepset (intersection)
- Family preservation: each potential is assigned to a cluster such that
- Cluster potential:
- ensure each is used once and only once
- Cluster graph
- Running intersection property
- for each pair of clusters and , there exists an unique path between fpr which all clusters and sepset contain
- a.k.a for any , the set of clusters & sepsets containing form a tree.
- If fulfilled by cluster tree, it is a junction tree
what can junstion tree do?
- Marginal probability on junction tree
- choose root clique
- inward message
- outward message
- messages:
- : random variable that are in but not in , need to marginalize out
- : common random variables in both &
Constructing Junction tree
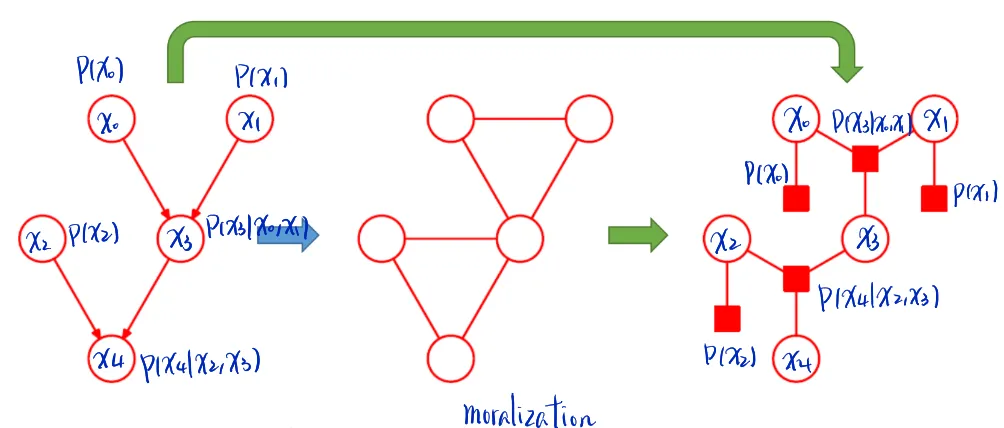
Triangulation: get reconstitution graph
- DAG to UAG to reconstitution graph
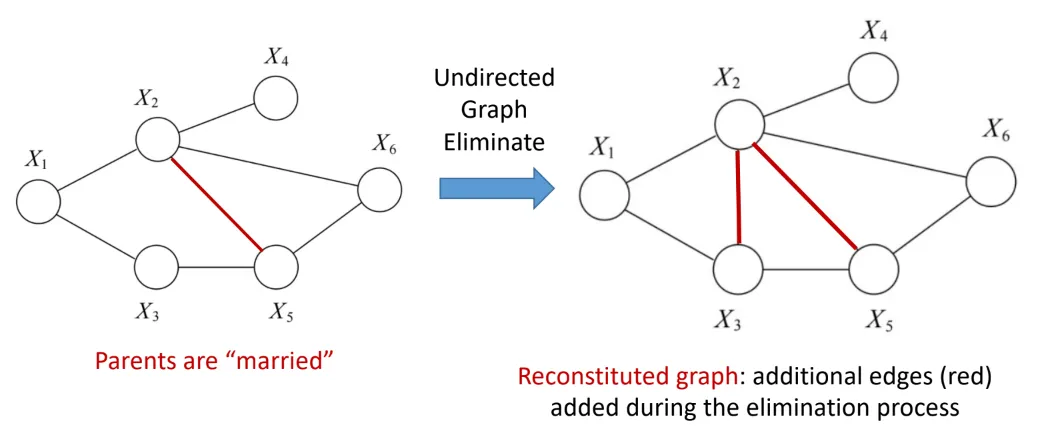
- DAG to UAG to reconstitution graph
Get all clusters and all possible sepsets
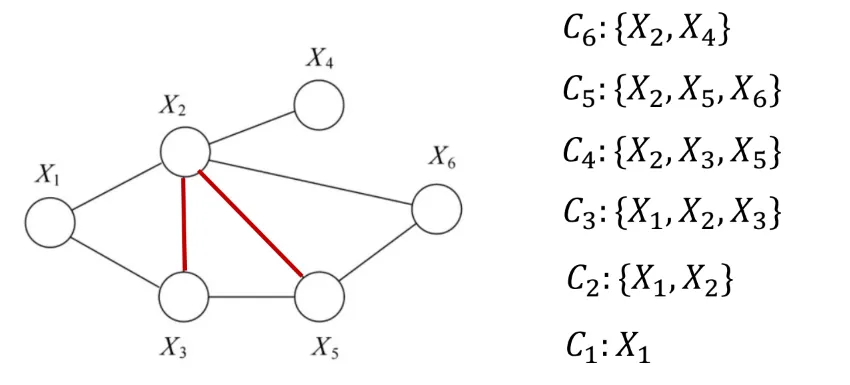
Assign cluster potentials
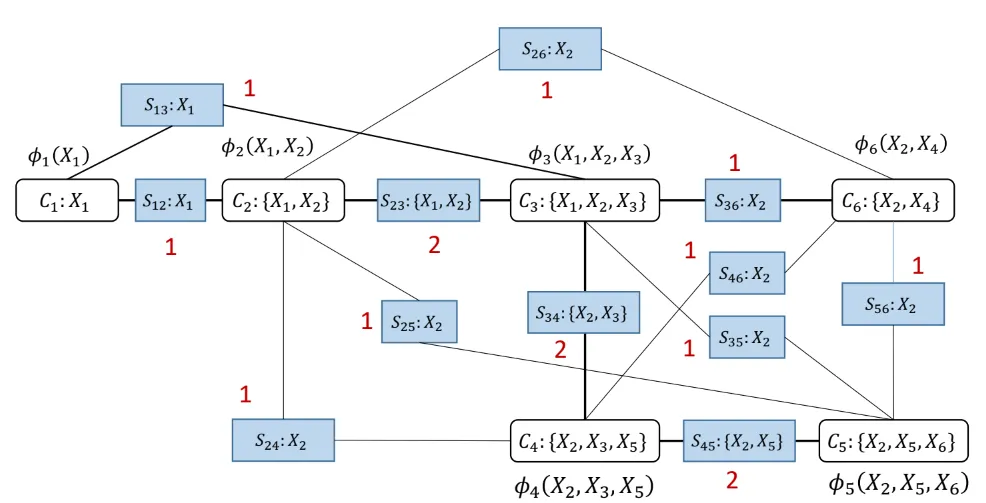
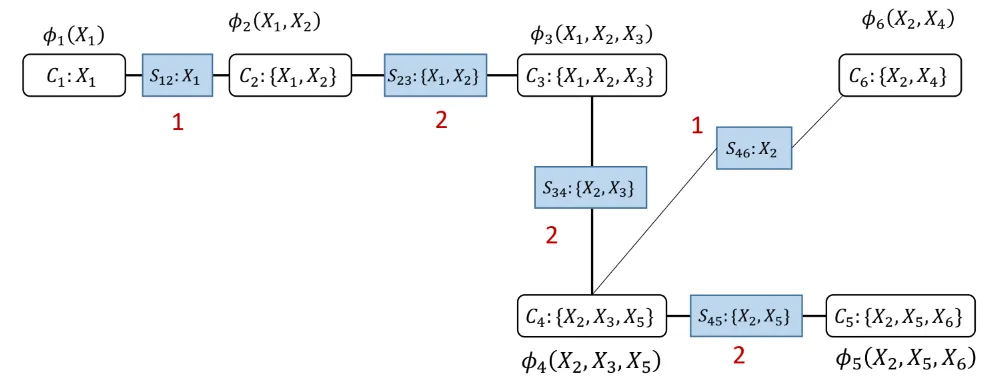
Get junction tree
- find the maximum spanning tree with weight cardinality of sepsets
TIP
A cluster tree is a junction tree only if it is a maximum spanning tree
[CS5340] Factor Graph & Junction Tree Algorithm
https://itsjeremyhsieh.github.io/posts/cs5340-5-factor-graph-and-junction-tree-algorithm/