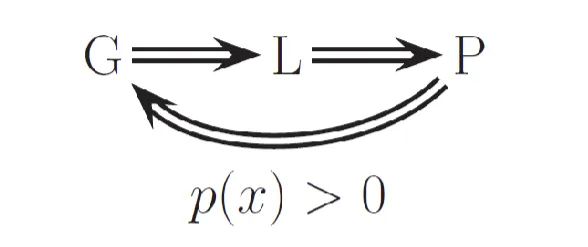Conditional Independence#

$x_a⊥x_c | x_b ⇨ \begin{cases} p(x_a,x_c|x_b)=p(x_a|x_b)p(x_c|x_b) \\ p(x_a|x_b,x_c) = p(x_a|x_b)\end{cases}$

5 Rules of Conditional Independence#

R1 Symmetry: $x⊥y ⇨ y⊥x$#

R2 Decomposition: $x⊥{A,b} ⇨ x⊥A$ & $x⊥b$#

• pf:
  $X⊥{A,B} ⇨ p(X,A,B) = p(X)p(A,B) \\ p(X,A) = \int p(X,A,B)dB = \int p(X)p(A,B)dB \\ = p(X) \int p(A,B)dB = p(X)p(A)$

R2 Reverse: $x⊥A$ & $x⊥b$ (DOESN”T hold)#

• pf:
  XOR Probability Counter-Example

R3 Weak Union: $X⊥{A,B} ⇨ X⊥A|B$ & $X⊥B|A$#

• pf: $X⊥{A,B} ⇨ p(X) = p(X|A,B)$
  $X⊥{A,B} ⇨ X⊥B$ $p(X) = p(X|A,B) = p(X|A)$, similar proof with $p(X|B)$

R3 Reverse: $X⊥A|B$ & $X⊥B|A$ ⇨ $X⊥{A,B}$#

• pf:
  $X ⊥ A | B \Rightarrow p(x|A,B) = p(x|B)$
  $X⊥B|A \Rightarrow p(x|A,B) = p(x|A)$
  $p(x) = \int p(x,A)dA = \int p(c|A)p(A)dA = p(x|A) \int p(A)dA = p(x|B)$

R4 Contraction: $X⊥A|B$ and $X⊥B ⇨ X⊥\{A,B\}$#

• pf:
  $X⊥A|B$ and $X⊥B ⇨ p(X|\{A,B\}) \\ = p(X|B) = p(X) ⇨ X⊥{A,B}$

R4 Reverse: $X⊥\{A,B\}$ ⇨ $X⊥A|B$ and $X⊥B$#

• pf:
  by weak union, $x⊥ \{A,B\}$ ⇨ $x⊥A|B$ by decomposition, $x⊥\{A,B\}$ ⇨ $x⊥B$

R5 Intersection: $X⊥Y|{W,Z}$ and $X⊥W|{Y,Z} ⇨ X⊥ {Y,W}|Z$#

• pf: $X⊥Y|{W,Z} ⇨ p(X|Y,W,Z) = p(X|W,Z)$
  $X⊥W|{Y,Z} ⇨ p(X|Y,W,Z) = p(X|Y,Z)$
  $p(X|W,Z) = p(X|Y,Z)$
  $p(X|Z) = \int p(X.W|Z)dW = \int p(X|W,Z)p(W|Z)dW = p(X|Y,Z \int p(W|Z)dW = p(X|Y,Z)$
  $p(X|W,Y,Z) = p(X|Y,Z) = p(X|Z) ⇨ X⊥{W,Y}|Z$

R5 Reverse: $X⊥ \{ Y,W \}|Z$ ⇨ $X⊥Y|{W,Z}$ and $X⊥W|{Y,Z}$#

• pf:
  $X⊥ \{ Y,W \}|Z \Rightarrow p(x|Z) = p(x|W,Y,Z)$
  $X⊥ \{ Y,W \}|Z \Rightarrow x⊥w|Z$ (decomposition)
  $p(x|Z) = p(x|W,Y,Z) = p(x|Y,Z) \Rightarrow x⊥W| \{ Y,Z \}$

Independence Map (I-Map)#

• $I(p)$ represents all independencies in $p(x_1, ..., x_N)$
• $G$ is valid if $I(G) \le I(P)$

Markov Property#

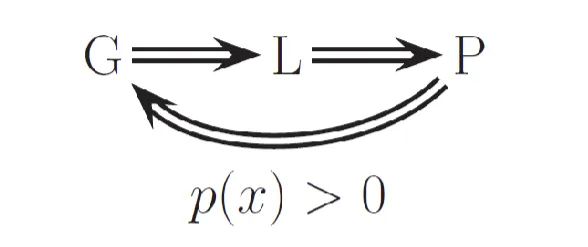
Global Markov Property#

• $x_A ⊥ x_B | x_C$ iff $C$ seperated $A$ from $B$
• 

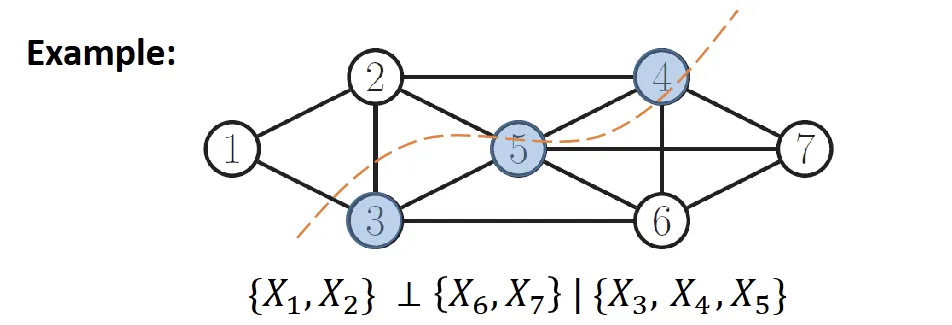
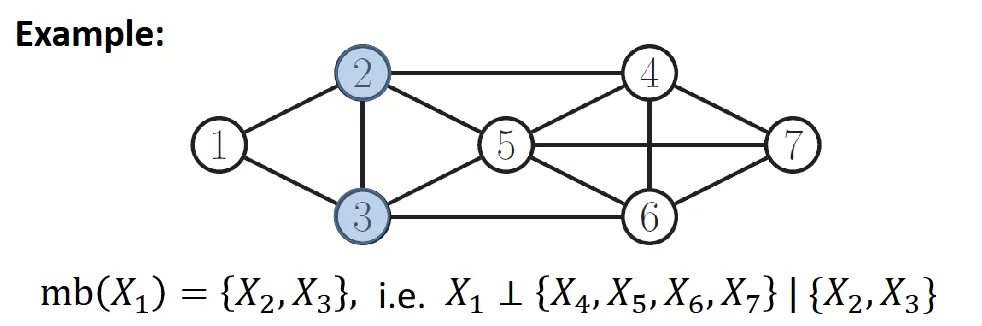
Local Markov Property#

• $x_S ⊥ V\backslash \{ mb(x_s), x_s\} | mb(x_s)$, where $mb(x_s)$ is the markov blanket of $x_s$
• 

Pairwise Markov Property#

• $x_s ⊥ x_t | v \backslash \{ x_s, x_t\}$
• $x_s, x_t$ condition independence given the rest if no direct edge between
• 

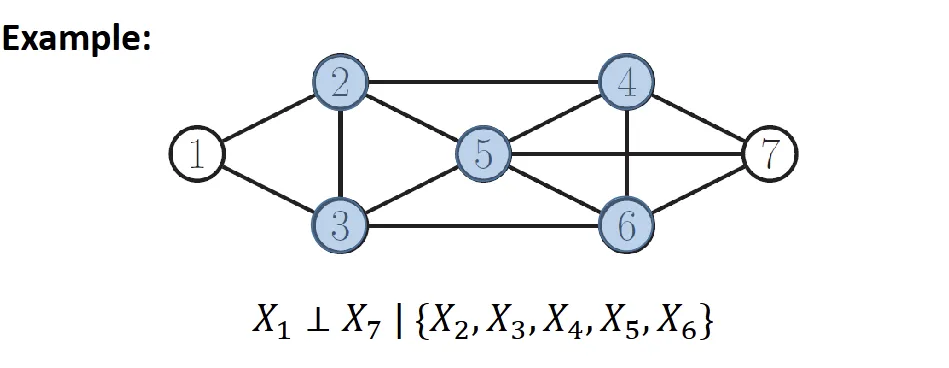
Parameterization of MRF#

• if $x$ and $y$ are not directed linked $\Rightarrow$ they are conditionally independent
  $\Rightarrow$ must place $x$ and $y$ in different factors (local functions)
• $𝜓(x_c)$: the local function of maximal clique $c$
• maximal clique: clique that cannot include additional nodes (fully connected subset of nodes)

Hammersley-Clifford Theorem#

• $p(y| \theta) = \frac {1}{Z(\theta)} \prod_c 𝜓_c(y_c| \theta_c$ (product of local function of max cliques)
  • $Z(\theta)$: for normalization (constant)

Log-Linear Potential Function (Maximum entropy)#

• $log p(y|\theta) = \sum_c \phi_c(y_c)^T \theta_c - log Z(\theta)$ (can reduce parameter)

Conditional Random Field (Discriminative random field)#

• $p(y | x,w) = \frac {1}{Z(x,w)} \prod_c 𝜓_c (y_c |x,w)$
• $𝜓_c (y_c |x,w) = \exp (w_c^T \phi (x,y_c)))$