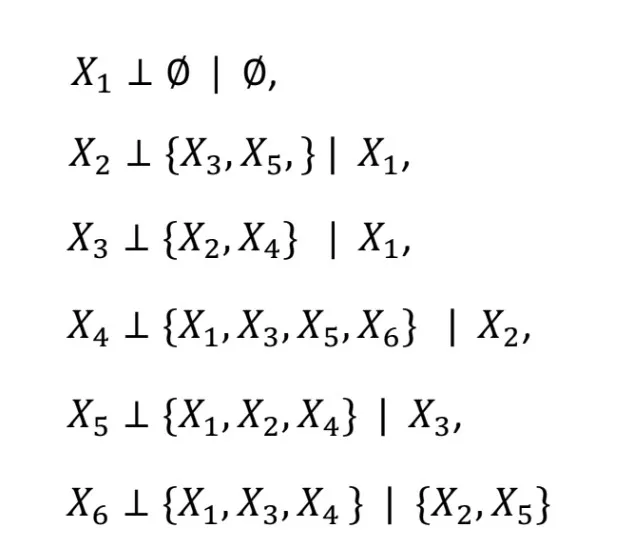Conditional Independence#
NOTERandom variables are often NOT fully independence, we use conditional independence to assume an intermediate degree of dependency among the random variables.
- Definition: xa⊥xc∣xb
- p(xa,xc∣xb)=p(xa∣xb)p(xc∣xb)
- p(xa∣xb,xc)=p(xa∣xb) (learning the values of xc does not change the prediction of xa once we know the value of xb)
Markov Assumption#
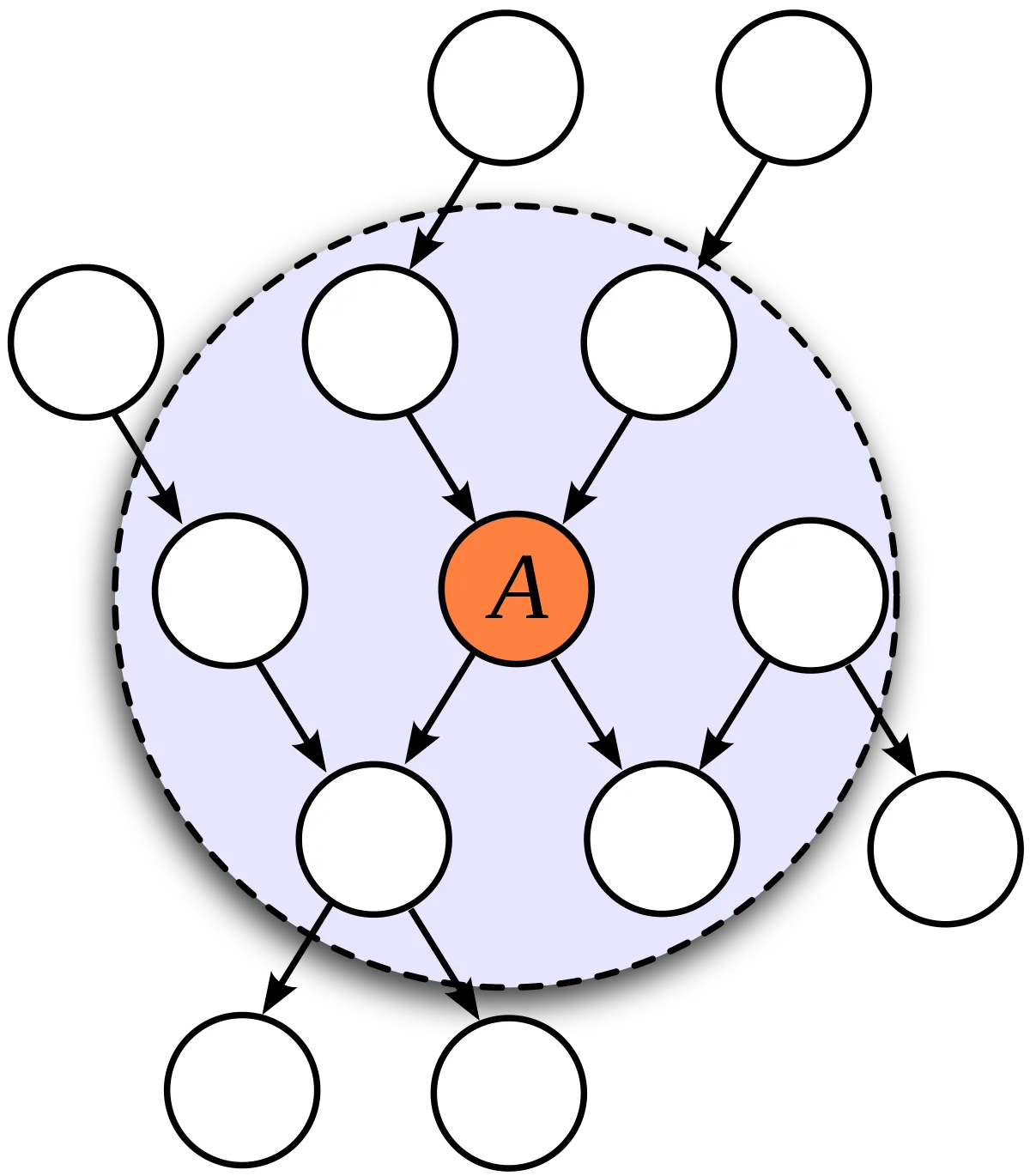
- xa⊥(xnonDesc−xparent)∣xparent
- xa is dependent only on its parents when given its parents
Parent-child relationship#
- p(xi∣xparent,(xnonDesc−xparent)=p(xi∣xparent)
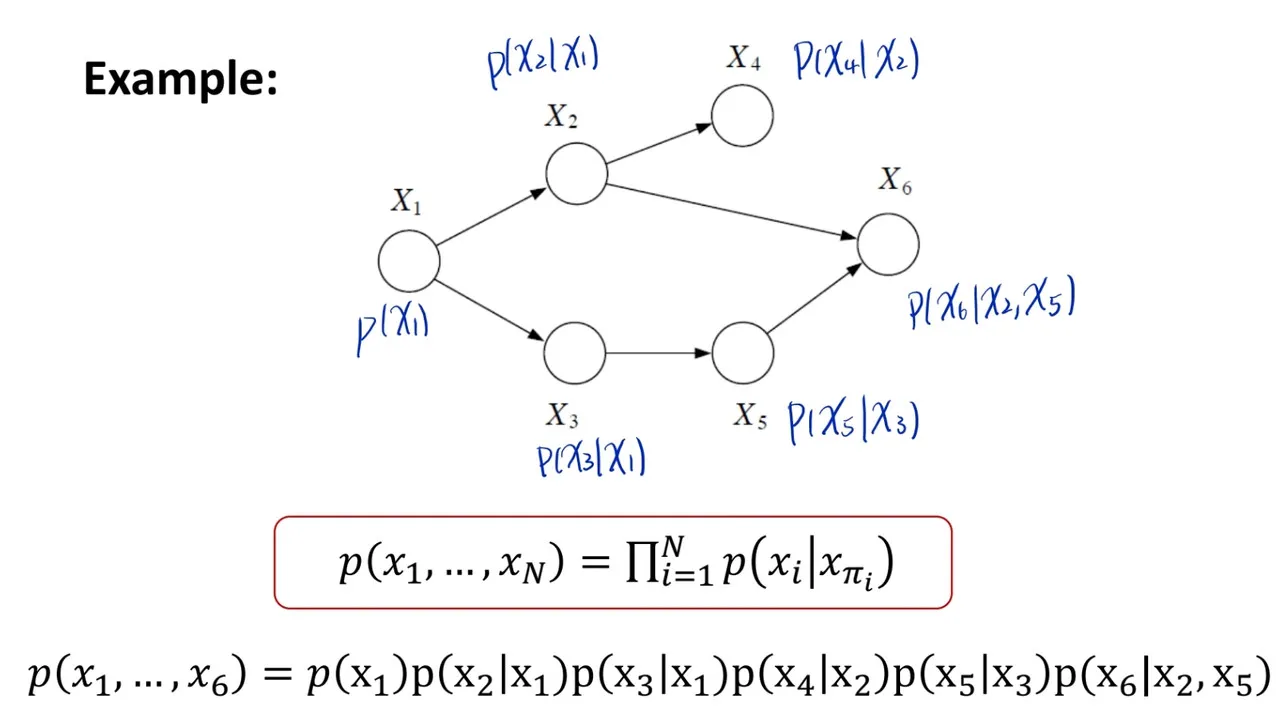
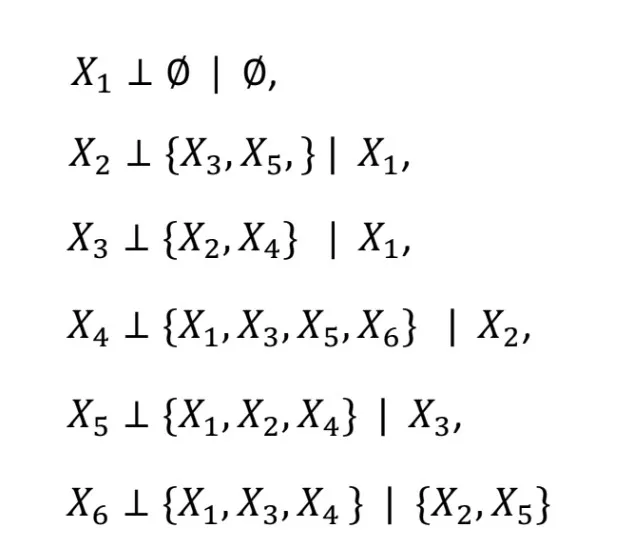
- by using parent-child relationship to represent **joint probability ** p(x1,x2,...,xn), parameter reduce from O(Kn) to O(Kmi+1), where "m" is the # of parent of node xi, and "+1" is xi itself
How can we find conditional independent directly from DGM?
Three Canonical 3-Node Graph#
Head-to-Tail#

- p(a,b,c)=p(a)p(c∣a)p(b∣c)
- No observation: p(a,b)=p(a)∑cp(c∣a)p(b∣c)
=p(a)∑cp(a)p(a)p(c∣a)p(b∣c)=p(a)∑cp(a)p(a,b,c)=p(b∣a)=p(a)p(b) - Observe c: p(a,b∣c)=p(c)p(a,b,c)=p(c)p(a)p(c∣a)p(b∣c)=p(c)p(c)p(a∣c)p(b∣c)=p(a∣c)p(b∣c), therefore A⊥B∣C
Tail-to-Tail#

- p(a,b,c)=p(a∣c)p(b∣c)p(c)
- No observation: p(a,b)=∑cp(a∣c)p(b∣c)p(c)=p(a)p(b)
- Observe c: p(a,b∣c)=p(c)p(a∣c)p(b∣c)p(c)=p(a∣c)p(b∣c), therefore A⊥B∣C
Head-to-Head (V-Structure)#

- p(a,b,c)=p(a)p(b)p(c∣a,b)
- No observation: p(a,b)=p(a)p(b)∑cp(c∣a,b)=p(a)p(b), therefore A⊥B
- Observe c: p(a,b∣c)=p(c)p(a)p(b)p(c∣a,b)
| Head-to-Tail | Tail-to-Tail | Head-to-Head |
|---|
| No observation | p(a,b)=p(a)p(b) | p(a,b)=p(a)p(b) | p(a,b)=p(a)p(b) |
| Observe middle node | p(a,b∥c)=p(a∥c)p(b∥c) (CI) | p(a,b∥c)=p(a∥c)p(b∥c) (CI) | p(a,b∥c)=p(a∥c)p(b∥c) (No CI) |
NOTEIf all paths from A to B are blocked by observing C, A is d-seperated from B by C ⇨ A⊥B∣C
How do we define “blocked”?
Bayes Ball Algorithm#
- reachability test
- If ball from node A cannot reach B by any path, then A⊥B∣C, else A⊥B∣C
Markov Blanket#
- Markov Blanket of node {x_i} comprised the set of parents, children & co-parents