373 words
2 minutes
[CS5340] Graph-Cut & Alpha-Expension
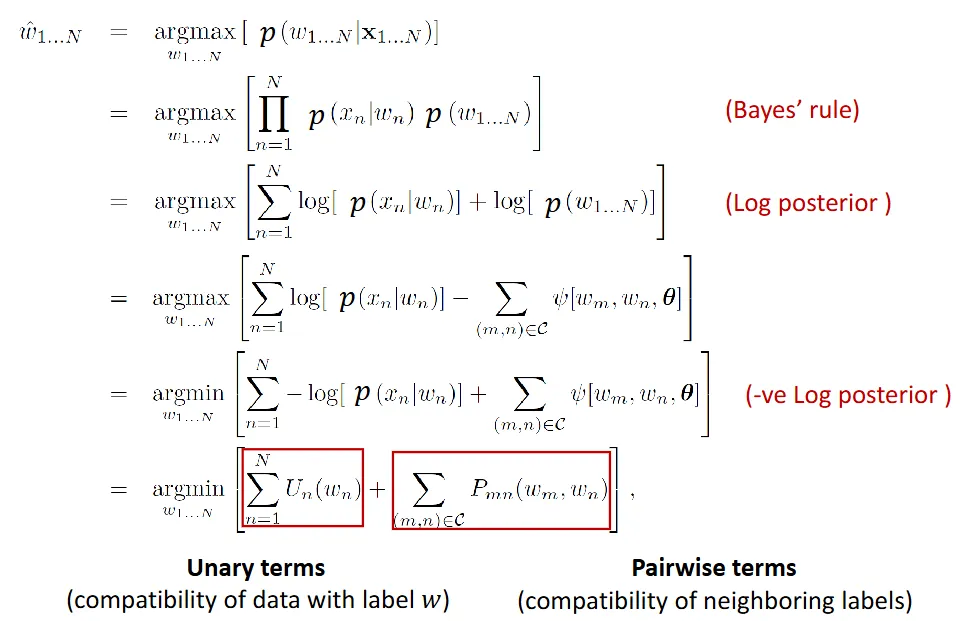
- Recover clean image pixels , given noisy observed data
- we want to:
- : encourage pixels () to stay the same label as observation ()
- : take the same label as neighbor ()
- cost function
Max-flow = Min-cut
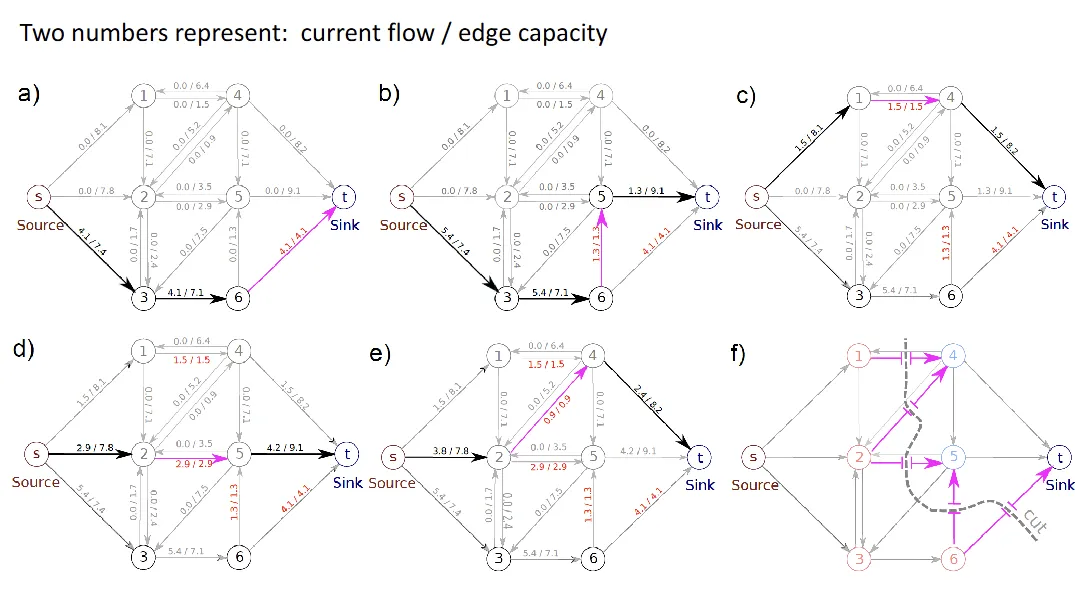
- a directed graph, a source, a sink
- capacity of an edge = max flow possible on the edge
- cut: node partition on graph
- capacity: sum of weights leaving
- flow: assignment of weights to edges
- (capacity)
- flow leaving flow entering
- Goal: find the flow that maximizes net flow
Observations
- net flow = flow entering
- value of flow capacity of the cut
- if capacity of the cut value of the flow, is max flow, is min cut
Residual Graph
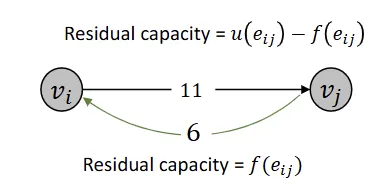
- undo flow sent
- augmenting path = path in residual graph
- if augmenting path exist: not a maz flow yet
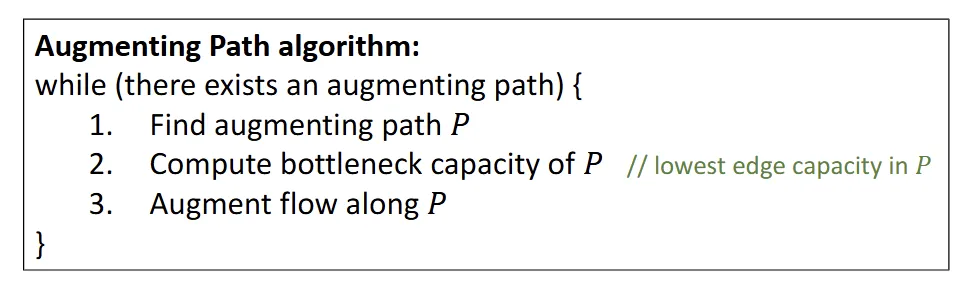
Augmenting Path Algorithm
Case 1: Binary MRF
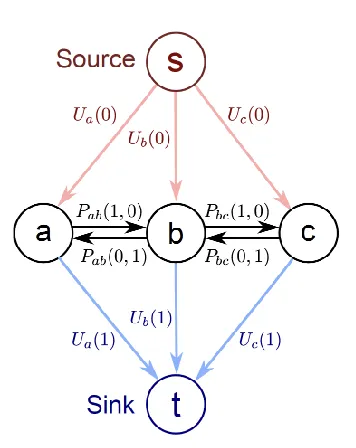
- Unary costs attached to links to source and to sink. Either one or the other is paid
- Pairwise costs between nodes, either one or the other is paid when and takes opposite labels.
- Reparameterization
- adjust the edge capacities so every possible solution is
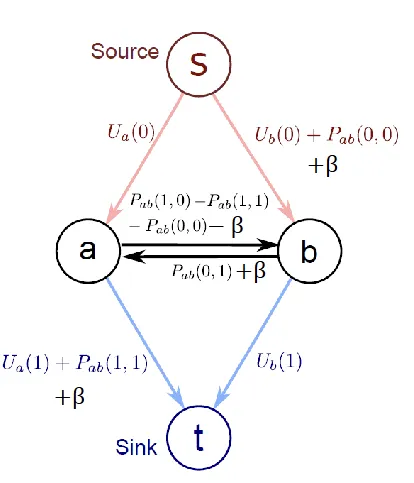
- adjust the edge capacities so every possible solution is
Submodularity
- if
- solve in polynomial time
Case 2: Multiple Labels (Submodular)

- Convex may over-smooth the image
Case 3: Multiple Labels (Non-submodular)
- Alpha-Expansion Algorithm
- breaks into binary sub-problems
- each step, choose an and expend, until no change
- each vertix is connected to &
- structure of graph is dynamix, changes depend on choice of
- 4 possible relationships
- have label , pairwise cost=0, only
- solution may be or (add new edge)
- solution may be , (no pairwise cost), (add ), (add )
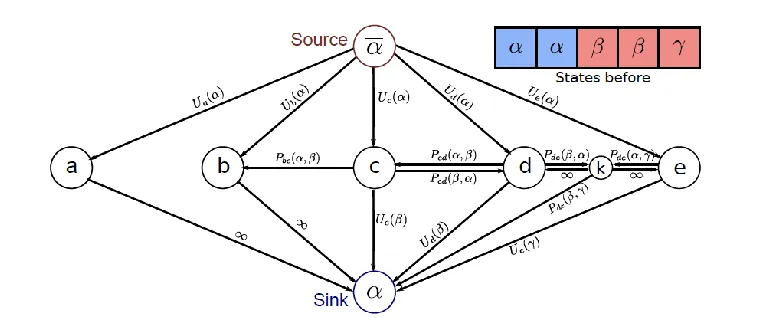
- solution may be , (no pairwise cost), (add ), (add )
- solution may be:
- (, add new edge between and sink)
- (, add new edge between and )
- (, add new edge between and )
- (no paiwise cost added)
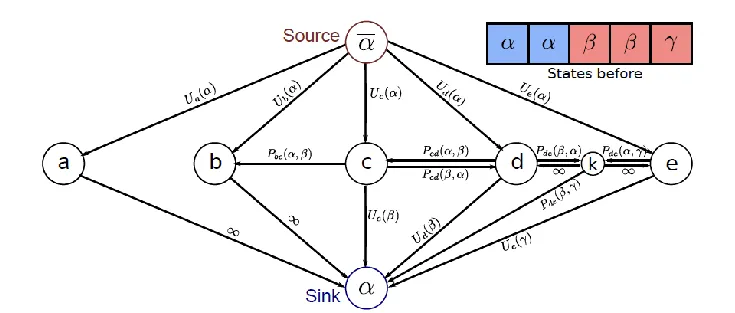
- solution may be:
- triangle inequality must hold
[CS5340] Graph-Cut & Alpha-Expension
https://itsjeremyhsieh.github.io/posts/cs5340-12-graph-cut-and-alpha-expension/