Discriminative model#

• posterior $p(C_k | X)$
• map $x$ to $C_k$ (class)

Generative model#

• likelihood $p(X|C_k)$
• sampling from the distribution
• can generate data points in input space
  • $p(x,z| \theta) = p(x|z, \theta) p(z)$
• 1. sampling from the prior $z ~ p(z)$ e.g: z = Bedroom
  2. generate new image from likelihood $p(x| z = Bedroom)$
• define prior $p(z)$, deterministic function $f(z ; \theta): z \times \theta \rightarrow x$
• optimize $\theta$: maximize likelihood $p(x| \theta) = \inf p(x|z, \theta) p(z) dz$, where $p(x|z, \theta) = N(x | f(z, \theta), \sigma^2I)$
  • but $z$ is high dimension, intractable
  • we suppose $p(z) = N(0,I)$
  • learn $f(z, \theta)$ in deep neural network

$f(z ; \theta): z \times \theta \rightarrow x$#

• consider $ln p(x | z, \theta) = ln N(x| f(z; \theta), \sigma^2I) = - | x-f(z; \theta)|^2 + const.$
• $ln p(x) = \sum_z q(z|x) ln p(x)$ (encoder) $= \sum_z q(z|x) ln \frac {p(x,z)}{q(z|x)}$ which is the lowerbound ($L(q, \theta)$) $+ \sum_z q(z|x) ln \frac {q(z|x)}{p(z|x)}$ (is the $KL[q(z|x) || p(z|x)] \geq 0$)

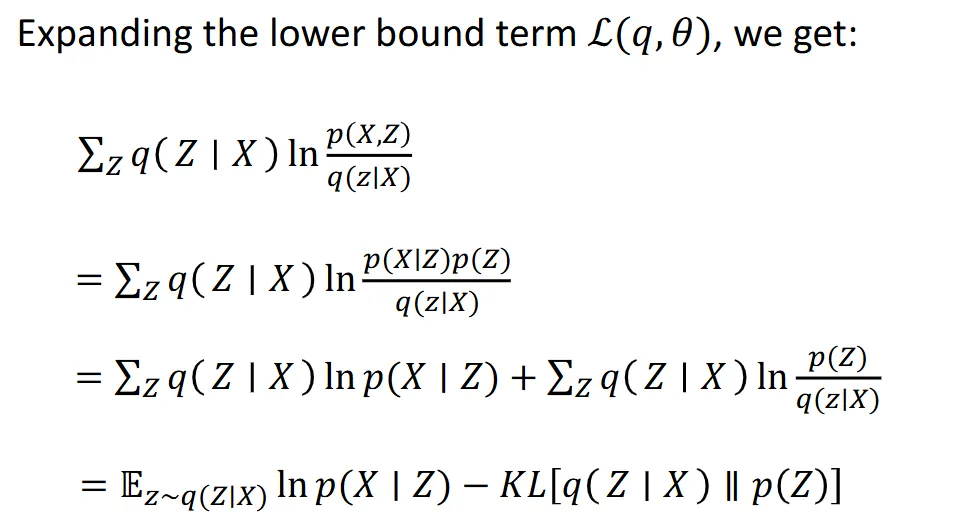
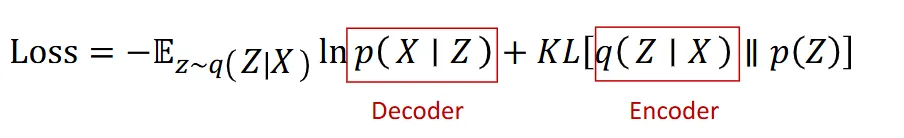
• but gradient $= \triangledown (ln p(x|z)) - KL[q(z|x) || p(z)]]$
  • $q(z|x)$ is not trained

Reparameterization Trick#

Diffusion Model#

• Encoder: data sample $x$, map it through a series of intermediate latent variables. (add noise)
  • no learning
  • $x \rightarrow Z_1 \rightarrow Z_2 \rightarrow ... \rightarrow Z_T$
• Decoder: starting with $Z_T$, map back to $x$
  • deep network
  • $Z_T \rightarrow Z_{T-1} \rightarrow ... \rightarrow Z_1 \rightarrow x$

Encoder (Diffusion)#

• $Z_1 = \sqrt {1- \beta_1} \times x + \sqrt {\beta_1} \times \epsilon_1$ (noise from normal distribution)

• $Z_t = \sqrt {1- \beta_t} \times Z_{t-1} + \sqrt {\beta_t} \times \epsilon_t$

• $\Rightarrow q(Z_1|x) = Norm[\sqrt {1-\beta_1} x, \beta_1 I]$
  $q(Z_{1 ...T}|x) = q(Z_1|x) \prod_{t=1}^T q(Z_t|Z_{t-1})$

• we want to get $z_t$ directly from $x$

• $Z_t = \sqrt {\alpha_t} \times x + \sqrt {q-\alpha_t} \times \epsilon$, $\alpha_t = \prod_{s=1}^t 1-\beta_s$

• $q(Z_t|x) = Norm_{Z_t} [\sqrt{\alpha_t} \times x, (q - \alpha_t)I]$

Decoder (learn the reverse process)#

• approx $Pr(Z_T) = Norm_{Z_T} [0,T]$
  $Pr(Z_t-1| Z_t, \phi_t) = Norm_{Z_{t-1}} [f_t[Z_t, \phi_t], \sigma_t^2I]$
  $Pr(x| Z_1, \phi_t) = Norm_{x} [f_1[Z_1, \phi_1], \sigma_1^2I]$
• 
• final lost function: