Convolution#

• Linear transformation
• Feature extraction
• 1D: Text, 2D: Image, 3D: microscopy …
• 

Why convolution?

• Sparse connection: each output only connect to inputs in reception field
  • fewer parameters, less overfitting
• Weight sharing (use the same kernel weight)
  • regularization, less overfitting
• Location/ Spatial invariant
  • same prediction for same input no matter where

1D Convolution#

• $y = \sum_{i=0}^{k-1} w_i \times x_{t+i}$
  • $w$: kernel/ filter (weights to be trained)
  • $x$: input
  • $y$: output feature
  • applied area = receptive field: generate one output value
• 

Padding#

What to do with boundary cases?

• determine edge values
• we want all elements to be processed the same # of time
• we also want output size = input size

pad with extra values (0)#

• without padding: $Output = input - kernal + 1$
• with padding: $Output = (input + padding) - kernal + 1$
• => same padding: $padding = kernal - 1$

Stride#

How to make training faster?

• steps to skip
• consecutive: stride = 1
• $s>1$: skip some elements
  • faster, efficive
• $Output = \lfloor \frac {input + padding - kernal}{stride}\rfloor + 1$
• same padding:
  • $\lfloor \frac {input + padding - kernal}{stride}\rfloor ≥ Output - 1$
    $padding ≥ stride \times (\lceil \frac {Output} {stride}\rceil - 1) + kernal - input$
    => $padding = max(stride \times (\lceil \frac {Output} {stride}\rceil - 1)+ kernal - input, 0)$

2D Convolution#

• Shape:
  • input = $n_h \times n_w$
  • kernal = $k_h \times k_w$
  • output = $O_h \times O_w$ = $(\lfloor \frac {n_h+p_h-k_h}{s_h}\rfloor + 1, \lfloor \frac {n_w+p_w-k_w}{s_w}\rfloor + 1)$
• Computational cost: $O(k_w \times k_h \times O_w \times O_h)$
• Multiple kernels: different levels of information (local vs. global)
• Multiple channels: results for all channels are summed (e.g RGB)

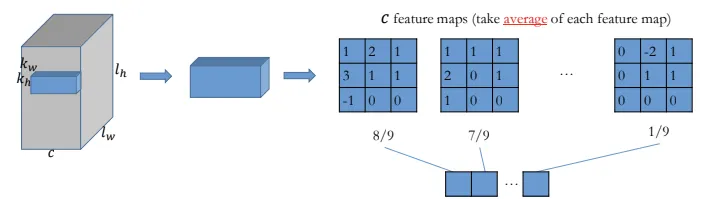
Pooling#

What to do for reducing size?

• Aggregrate information from each receptive field
  • average, maximum
• No parameter
• Applied for each channels respectively
• Reduces feature/ model size
• Invariant to rotation of input
• e.g Average pooling