Activation Function $g()$#

• perform non-linear feature transformation
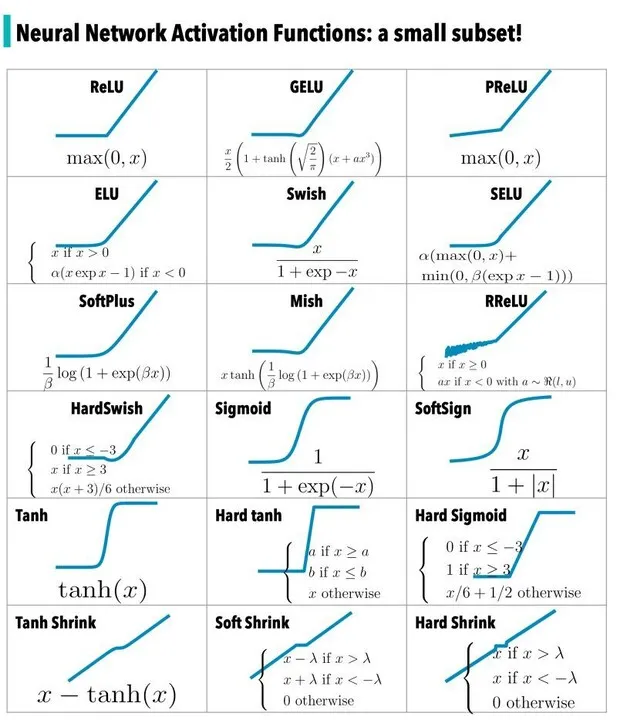
  • e.g
• non-linear because linear is too limited
  • many linear layers can collapse into one single layer
• $Z^i = w^ih^{i-1} + b^i$
  $h^i = g^i(Z^i)$, where $g^i$ is the non-linear activation function

Stochastic Gradient Discent#

• Problems with GD:

  • Local Optimum: cannot update weights, so next gradients are also 0, each iteration use same (whole) dataset, so there’s no way it can escape
  • Efficiency: GD has to load all training samples

• randomly pick a (single)training sample to perform BP

  • mode efficient
  • but much slower, needs more iterations to train

• Mini-batch SGD: randomly pick $b$ training samples

• Converge rate: $R_{GD} > R_{mini-SGD} > R_{SGD}$

• Time per iteration: $T_{GD} > T_{mini-SGD} > T_{SGD}$

• Training time = $T/R$

• AdaGrad: change learning rate according to gradient

• RMSProp: rescale learning rate to remove effect of gradient size, balance between different directions

  • $S = \beta s + (i- \beta) g^2$, $s$ has history information,
    $w = w - \frac {\alpha g}{\sqrt {\hat S + \epsilon}}$, $g$ has current information, $\beta$ to balance

• Adam: combining momentum and RMSProp

  • $v = \beta_1 v + (1- \beta_1)g$
    $s = \beta_2 s + (1- \beta_2)g$
    $w = w - \alpha \frac {\hat v}{\sqrt {\hat s + \epsilon}}, \hat v = \frac {v}{1-\beta_1}, \hat s = \frac {s}{1- \beta_2}$