The Perceptron#

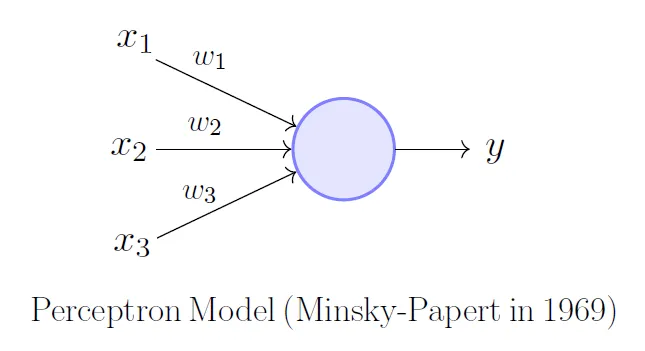
• algorithm to perform image classification

Multi-layer Perceptron (MLP)#

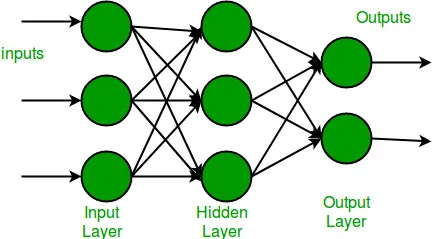
• with fully connected layers

Gradient Descent#

1. Predict
   • Forward pass: $\tilde y = w x_i$
   • Compute loss: $L_i = \frac {1}{2}(y_i- \tilde y)^2$ (L2 loss function)
2. Update
   • Backward propogation: $\frac{\partial L_i}{\partial w} = -(y_i - \tilde y) x_i = ▽w$
   • Gradient update: $w = w - ŋ▽w$

Under/ Over fitting#

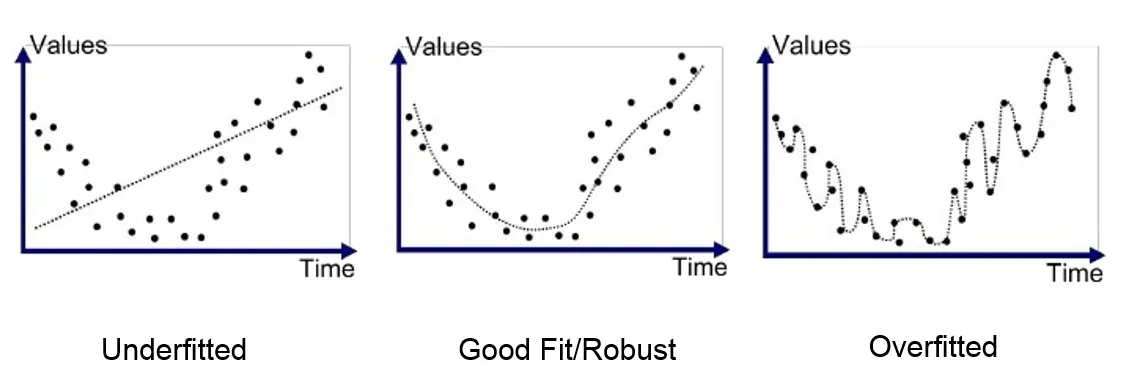
• Underfitting:
  • Low model complexity => too simple to fit data
  • High bias (constently learn wrong thing)
• Overfitting:
  • High model complexity => fits too well to seen data
  • High variance (amount of parameter change for different training data)
  • Cannot generalize onto new unseen data)

Data Splitting#

• Training set for model training
• Validation set for model tuning
• Testing set for testing the final model

K-fold cross validation#

• if only few training data
• Divide training set into $K$ partitions
• $K-1$ for training, $1$ for validation
• Repeat $k$ times

Cross entropy loss function#

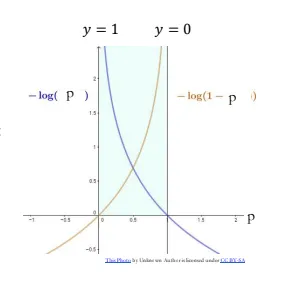
• for ** classification**
• Entropy: the degree of randomness (uncertainty)
  • $H(x) = - \sum p(x) log p(x)$
  • the grater the more uncertain
• $L = \frac {1}{n} [\sum_{j=1}^N [t_j log(p_j) + (1-t_j) log (1-p_j)]]$, $t_j$: the true value ${0,1}$
  • if $y=1$ => $L=-log(p)$
  • if $y=0$ => $L=-log(1-p)$